Notação
Os primeiros a utilizarem a letra grega
 foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.
foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.Valor de π
O valor de π pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar π por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima π por 3,1415927. Para cálculos mais precisos pode-se utilizar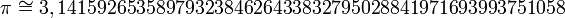 com 52 casas decimais.Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais.
com 52 casas decimais.Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais.Aproximações para π
Desde a Antiguidade, foram encontradas várias aproximações de π para o cálculo da área do círculo. Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a π seria , embora também seja encontrado o valor
, embora também seja encontrado o valor  . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor
. Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor 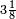 já ser conhecido como aproximação.
já ser conhecido como aproximação.Métodos de cálculo
Existem muitas formas de se obter o valor exato de π e alguns métodos aproximados. Consideramos que [[π]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.Método clássico para o cálculo de π
A primeira tentativa rigorosa de encontrar π deve-se a um dos mais conhecidos matemáticos da Antigüidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.[8]Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou pi tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.
A "busca" pelo valor de π chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung-chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62.000. O resultado é aproximadamente uma circunferência de diâmetro 20.000".
Analisando matematicamente e considerando a equação citada anteriormente de
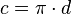 :
:O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de π com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de π com as supracitadas 35 casas decimais.
Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para π.
Uma aproximação de π que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:
Formulação matemática do método de Arquimedes
Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:
a2 = b2 + c2 − 2bccosα
Temos formado um triângulo isósceles, de base l e lados r=1:
l2 = r2 + r2 − 2r2cosα
l2 = 12 + 12 − 2cosα
l2 = 2 − 2cosα

O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:

Dessa forma, o perímetro do polígono será de:

Como π é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:

Aplicanto transformações trigonométricas, a fómula acima pode ser simplificada para:

Métodos estatísticos
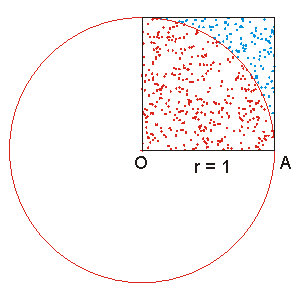
Outro método interessante para o cálculo de π pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas O = (0,0) e B = (1,1). Em seguida calcula-se a distância dos pontos sorteados cn = (xn,yn) até a origem O = (0, 0). π pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.No exemplo ao lado ,

Outro método que utiliza a estatística de Monte Carlo para o cálculo de π é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.
Métodos de séries infinitas
O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de π em 1593: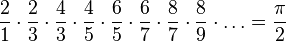 .
.
 .
.
Métodos de cálculo numérico
Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função f(x) = sin(x) sabemos que f(π) = sin(π) = 0. Os principais métodos do calculo numérico para a obtenção da raiz da função f(x) podem incluir uma busca binária no intervalo [a,b] onde se sabemos que f(3) = sin(3) > 0 (a = 3) e f(4) = sin(4) < 0 (b = 4) então podemos aprimorar o intervalo para:-
![[a, {{a+b} \over 2}]](http://upload.wikimedia.org/math/5/4/0/54038e4a1419787a59fba6fc401068cd.png) , se
, se  e
e
-
![[{{a+b} \over 2}, b]](http://upload.wikimedia.org/math/9/6/1/961d4408cc3436372b070876103e77dc.png) , se
, se 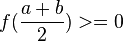
![\pi \in [3, 4]](http://upload.wikimedia.org/math/5/c/0/5c0a97ccaab358bec9a15560fa5502a2.png) esse método permite refiná-lo sucessivamente para os intervalos
esse método permite refiná-lo sucessivamente para os intervalosAinda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função f(x) = sin(x) utilizando um ponto inicial x0 exigindo que conheçamos f'(x) = cos(x).
Tomando-se x0 = 3 e considerando-se que por Newton-Rapson
-
 ,
,
- x0 = 3
- x1 = 3,14254654
- x2 = 3,14159265
-
- xi + 1 = xi + sin(xi),
 .
.Notemos que nesses algoritmos de cálculo numérico considera-se π como trancendental, uma vez que a função f(x) = sin(x) não pode ser escrita através de um polinômio finito de coeficientes racionais; a função f(x) = sin(x) é obtida através da expansão da série de Taylor.







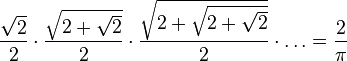
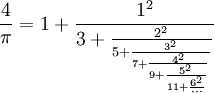
![\pi \in [3, 3.5]](http://upload.wikimedia.org/math/2/3/8/238996635809270862ab2383deee77d5.png)
![\pi \in [3, 3.25]](http://upload.wikimedia.org/math/6/c/8/6c886c5cc20f48284c9417fb4ecf6864.png)
![\pi \in [3.125, 3.25]](http://upload.wikimedia.org/math/3/5/1/3516956016d85ced87e5cb01becc1b41.png)
![\pi \in [3.125, 3.1875]](http://upload.wikimedia.org/math/0/9/c/09cb9699db5827df881ed3e4afcebde8.png)
Nenhum comentário:
Postar um comentário