Como Aplicamos o Número Pi no Dia-a-Dia
Nos usamos o numero pi para medir comprimento de uma circunferência e d o diâmetro, temos:
c/d = pi
c = pi x d Como o comprimento de uma circunferência é dado por c = pi . d, é fácil entender que a solução da equação de Aryabhata:
(4 + 100) x 8 + 62 000 = pi x 20 000
104 x 8 + 62 000 = pi x 20 000
832 + 62 000 = pi x 20 000
62 832 = pi x 20 000
62 832/20 000 = pi
3,1416 = pi
Quanto maior o número de casas decimais, melhor é a aproximação que se obtém para pi.
Há pessoas que têm inventado frases, em diferentes línguas, para ajudar a memorizar π, em que o número de letras de cada palavra indica o respectivo algarismo. Por exemplo:
“Sou o medo e temor constante do menino vadio” – 3,14159265
“Que j’aime à faire apprendre un nombre utile aux sages” - 3,1415926535
“May I have a large container of coffee” - 3,1415926
Existem muitas formas de se obter o valor exato de π e alguns métodos aproximados. Consideramos que [[π]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de π com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de π com as supracitadas 35 casas decimais.
Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para π.
Uma aproximação de π que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:
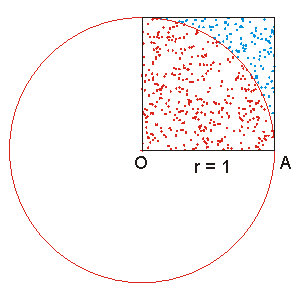
Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.
Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:
a2 = b2 + c2 − 2bccosα
Temos formado um triângulo isósceles, de base l e lados r=1:
l2 = r2 + r2 − 2r2cosα
l2 = 12 + 12 − 2cosα
l2 = 2 − 2cosα
O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:
O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de π em 1593:
Outra série conhecida para o cálculo de π foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)=π/4.
Johann Heinrich Lambert publicou, em 1770, uma série na forma de divisões infinitas:
Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função f(x) = sin(x) sabemos que f(π) = sin(π) = 0. Os principais métodos do calculo numérico para a obtenção da raiz da função f(x) podem incluir uma busca binária no intervalo [a,b] onde se sabemos que f(3) = sin(3) > 0 (a = 3) e f(4) = sin(4) < 0 (b = 4) então podemos aprimorar o intervalo para:
Partindo-se do intervalo \pi \in [3, 4] esse método permite refiná-lo sucessivamente para os intervalos
e assim sucessivamente.
Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função f(x) = sin(x) utilizando um ponto inicial x0 exigindo que conheçamos f'(x) = cos(x).
Tomando-se x0 = 3 e considerando-se que por Newton-Rapson
temos a seguinte série para π
1. x0 = 3
2 . x1 = 3,14254654
2. x2 = 3,14159265
Um método otimizado de cálculo numérico para o cálculo de π através das raízes de uma função pode ser obtido pela simplificação
xi + 1 = xi + sin(xi),
pois na proximidade de π,
Notemos que nesses algoritmos de cálculo numérico considera-se π como trancendental, uma vez que a função f(x) = sin(x) não pode ser escrita através de um polinômio finito de coeficientes racionais; a função f(x) = sin(x) é obtida através da expansão da série de Taylor.
O numero pi é igual a : 0,3333333... = 0,3
1,6666666... = 1,6
12,121212... = 12,12
0,9999999... = 0,9
7,1333333... = 7,13
0,333333... = 0,(3) = 0,3
3,636363... = 3,(63) = 3,63
c/d = pi
c = pi x d Como o comprimento de uma circunferência é dado por c = pi . d, é fácil entender que a solução da equação de Aryabhata:
(4 + 100) x 8 + 62 000 = pi x 20 000
104 x 8 + 62 000 = pi x 20 000
832 + 62 000 = pi x 20 000
62 832 = pi x 20 000
62 832/20 000 = pi
3,1416 = pi
Quanto maior o número de casas decimais, melhor é a aproximação que se obtém para pi.
Há pessoas que têm inventado frases, em diferentes línguas, para ajudar a memorizar π, em que o número de letras de cada palavra indica o respectivo algarismo. Por exemplo:
“Sou o medo e temor constante do menino vadio” – 3,14159265
“Que j’aime à faire apprendre un nombre utile aux sages” - 3,1415926535
“May I have a large container of coffee” - 3,1415926
Existem muitas formas de se obter o valor exato de π e alguns métodos aproximados. Consideramos que [[π]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de π com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de π com as supracitadas 35 casas decimais.
Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para π.
Uma aproximação de π que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:
Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.
Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:
a2 = b2 + c2 − 2bccosα
Temos formado um triângulo isósceles, de base l e lados r=1:
l2 = r2 + r2 − 2r2cosα
l2 = 12 + 12 − 2cosα
l2 = 2 − 2cosα
O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:
O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de π em 1593:
Outra série conhecida para o cálculo de π foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)=π/4.
Johann Heinrich Lambert publicou, em 1770, uma série na forma de divisões infinitas:
Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função f(x) = sin(x) sabemos que f(π) = sin(π) = 0. Os principais métodos do calculo numérico para a obtenção da raiz da função f(x) podem incluir uma busca binária no intervalo [a,b] onde se sabemos que f(3) = sin(3) > 0 (a = 3) e f(4) = sin(4) < 0 (b = 4) então podemos aprimorar o intervalo para:
Partindo-se do intervalo \pi \in [3, 4] esse método permite refiná-lo sucessivamente para os intervalos
e assim sucessivamente.
Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função f(x) = sin(x) utilizando um ponto inicial x0 exigindo que conheçamos f'(x) = cos(x).
Tomando-se x0 = 3 e considerando-se que por Newton-Rapson
temos a seguinte série para π
1. x0 = 3
2 . x1 = 3,14254654
2. x2 = 3,14159265
Um método otimizado de cálculo numérico para o cálculo de π através das raízes de uma função pode ser obtido pela simplificação
xi + 1 = xi + sin(xi),
pois na proximidade de π,
Notemos que nesses algoritmos de cálculo numérico considera-se π como trancendental, uma vez que a função f(x) = sin(x) não pode ser escrita através de um polinômio finito de coeficientes racionais; a função f(x) = sin(x) é obtida através da expansão da série de Taylor.
O numero pi é igual a : 0,3333333... = 0,3
1,6666666... = 1,6
12,121212... = 12,12
0,9999999... = 0,9
7,1333333... = 7,13
0,333333... = 0,(3) = 0,3
3,636363... = 3,(63) = 3,63
 foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi
foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi 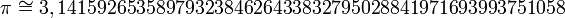 com 52 casas decimais.Para cálculos ainda mais precisos pode-se obter aproximações de
com 52 casas decimais.Para cálculos ainda mais precisos pode-se obter aproximações de  , embora também seja encontrado o valor
, embora também seja encontrado o valor  . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de
. Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de 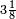 já ser conhecido como aproximação.
já ser conhecido como aproximação.
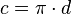 :
:











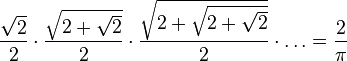
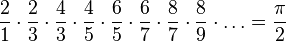 .
.  .
. 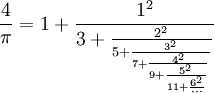
![[a, {{a+b} \over 2}]](http://upload.wikimedia.org/math/5/4/0/54038e4a1419787a59fba6fc401068cd.png) , se
, se  e
e ![[{{a+b} \over 2}, b]](http://upload.wikimedia.org/math/9/6/1/961d4408cc3436372b070876103e77dc.png) , se
, se 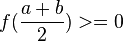
![\pi \in [3, 4]](http://upload.wikimedia.org/math/5/c/0/5c0a97ccaab358bec9a15560fa5502a2.png) esse método permite refiná-lo sucessivamente para os intervalos
esse método permite refiná-lo sucessivamente para os intervalos![\pi \in [3, 3.5]](http://upload.wikimedia.org/math/2/3/8/238996635809270862ab2383deee77d5.png)
![\pi \in [3, 3.25]](http://upload.wikimedia.org/math/6/c/8/6c886c5cc20f48284c9417fb4ecf6864.png)
![\pi \in [3.125, 3.25]](http://upload.wikimedia.org/math/3/5/1/3516956016d85ced87e5cb01becc1b41.png)
![\pi \in [3.125, 3.1875]](http://upload.wikimedia.org/math/0/9/c/09cb9699db5827df881ed3e4afcebde8.png)
 ,
,  .
.